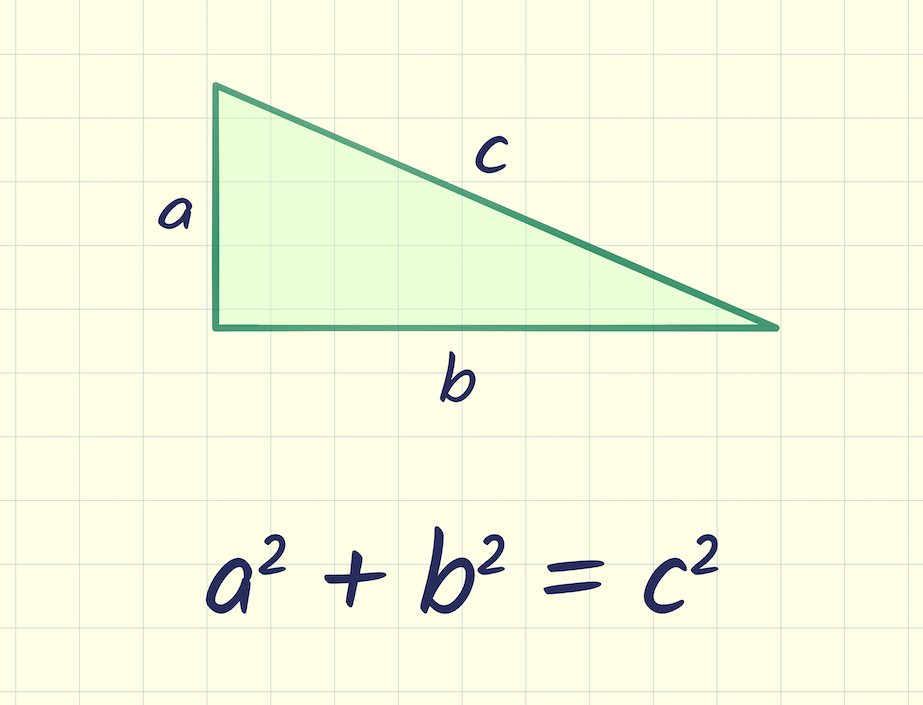
The Pythagorean theorem is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This can be written as an equation: $a^2+b^2=c^2$, where $a$ and $b$ are the lengths of the legs of the right triangle, and $c$ is the length of the hypotenuse [1] [2]. The theorem is named after the ancient Greek mathematician Pythagoras of Samos, who is traditionally credited with its first proof, although evidence suggests that the relationship was known much earlier in various ancient civilizations, including Babylonian, Egyptian, and Chinese cultures [3] [4].

According to www.iAsk.Ai - Ask AI:

The Pythagorean theorem has numerous applications beyond basic geometry, extending into fields such as trigonometry, physics, engineering, and even computer graphics [5]. For instance, it is crucial for calculating distances in a coordinate plane, as it forms the basis of the distance formula [6]. In physics, it's used to determine the magnitude of resultant vectors [7]. The theorem's converse is also true: if the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle [8]. This property allows for the identification of right angles in various practical scenarios.

Historical Context

While Pythagoras is often credited, the understanding of the relationship between the sides of a right triangle predates him. Ancient Babylonian tablets, such as Plimpton 322 (dating back to around 1800 BCE), contain lists of Pythagorean triples (sets of three integers $a,b,c$ such that $a^2+b^2=c^2$), indicating a sophisticated understanding of this mathematical concept [9]. Similarly, evidence from ancient Egypt suggests the use of ropes with knots to form 3-4-5 triangles, which are right triangles, for surveying and construction purposes [10]. The Zhoubi Suanjing, an ancient Chinese mathematical text, also presents a geometric proof of the theorem, known as the "Gougu theorem" in China, centuries before Pythagoras [11].

Proofs of the Pythagorean Theorem

There are hundreds of known proofs for the Pythagorean theorem, demonstrating its fundamental nature and versatility. One of the most common and intuitive proofs involves rearranging areas. Consider a large square with side length $(a+b)$. Inside this square, four right triangles with legs $a$ and $b$ and hypotenuse $c$ can be arranged, leaving a smaller square in the center with side length $c$. The area of the large square is $(a+b{)}^2$. The area of the four triangles is $4\times \frac{1}{2}ab=2ab$. The area of the inner square is $c^2$. Therefore, $(a+b{)}^2=4\times \frac{1}{2}ab+c^2$, which simplifies to $a^2+2ab+b^2=2ab+c^2$, and finally to $a^2+b^2=c^2$ [12]. Another well-known proof uses similar triangles, where the altitude to the hypotenuse divides the right triangle into two smaller triangles that are similar to the original triangle and to each other [13].

Applications

The Pythagorean theorem is indispensable in various fields:

• Construction and Architecture: Used to ensure square corners, calculate diagonal lengths, and determine roof pitches [14].
• Navigation: Essential for calculating distances and positions, particularly in two-dimensional space [15].
• Computer Graphics: Fundamental for calculating distances between points, rendering 3D objects, and performing transformations [16].
• Physics: Applied in vector addition, calculating magnitudes of forces, velocities, and displacements [17].
• Engineering: Used in structural analysis, design of mechanical components, and electrical circuit analysis [18].

Answer Provided by iAsk.ai – Ask AI.